March 2, 2022
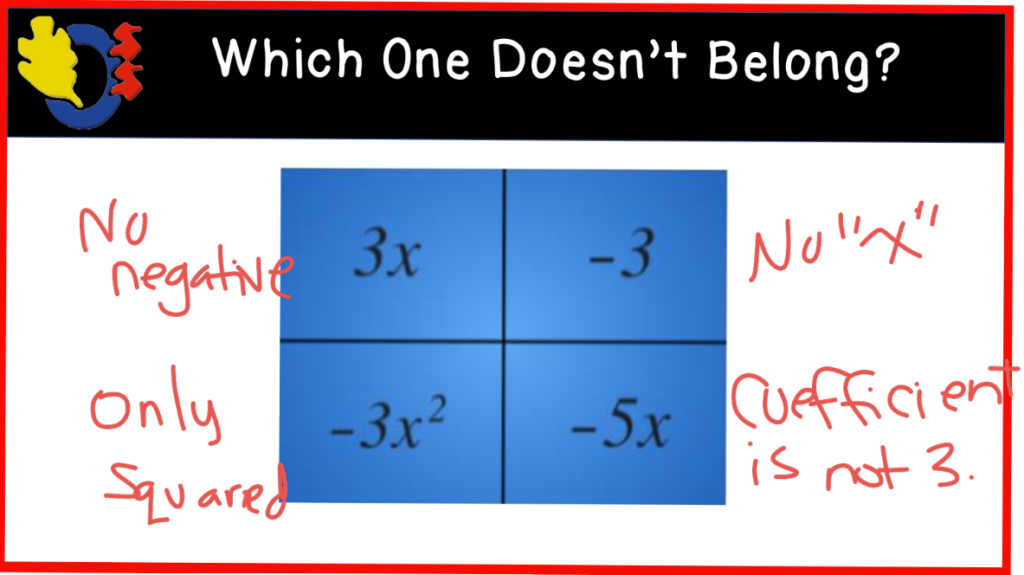
We started today’s lesson with a polynomial Which One Doesn’t Belong (WODB). Students had to think about a way to explain why each of the four quadrants didn’t belong. This was a great way to refresh the terminology that we have been using in class.

Next, we looked at a multiplying fractions example. We moved away from the area model method and jumped to the algorithm.
We talked about reducing the diagonals where possible to allow us to work with smaller numbers.

We then reviewed simplifying expressions using a chart to organize our thoughts. Students had not seen the coefficient in front of the bracket and were able to visualize what this meant. Although I had the algebra tiles available, this group didn’t want to get them out. We had them out yesterday, which helped a lot.
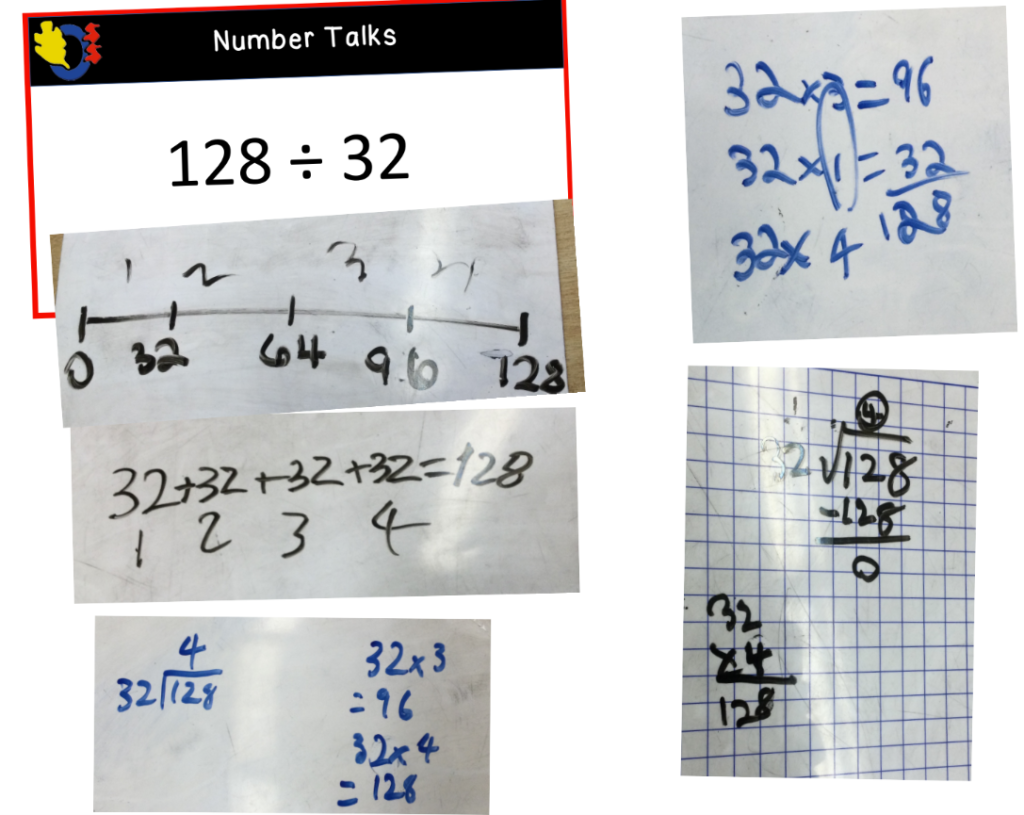
Next, we dove right into a “Number Talks” and the topic was division. I gave the students a straight forward division problem and asked them to answer the problem using a strategy or method of their choice. I was pleased with the variety of types of answers that students provided. It allowed for great conversation.

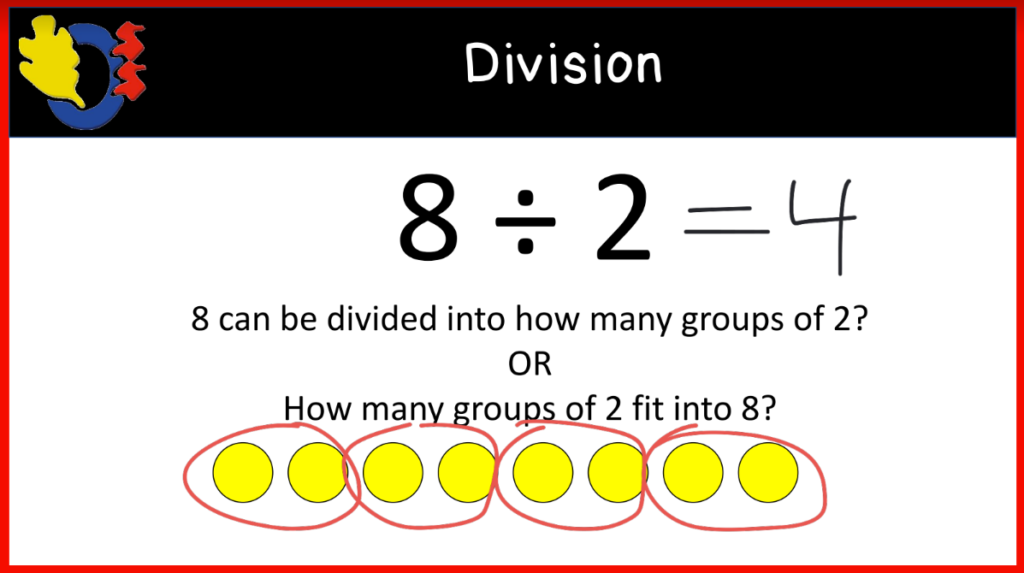
We then looked at dividing fractions. We started by discussing some simple problems and talked about how many groups we could make. For the first problem, I asked the students how many groups of 2 fit into the number 8? We used coloured tiles to help model and represent the problem. Next we looked at an example with a fraction. How many groups of 1/2 could fit into 8?

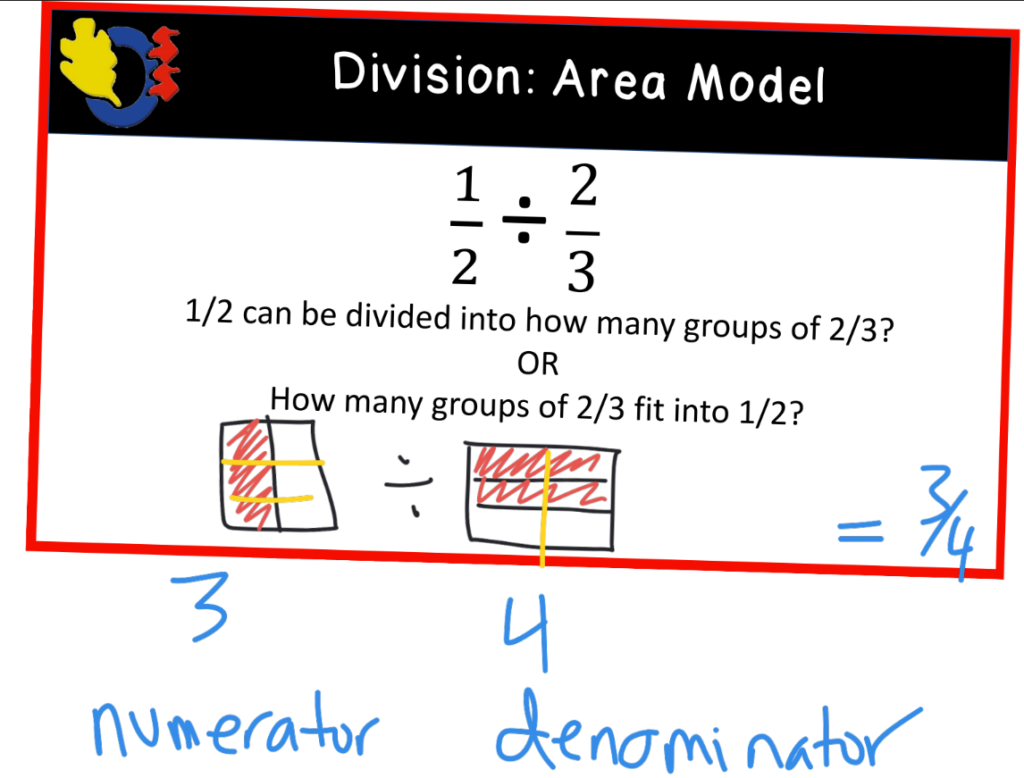
Finally, We revisited the area model and brought out the “brownie pans”. For the next three questions, we looked at dividing two fractions. We shaded 1/2 of the first brownie pan and 2/3 of the second brownie pan. Next we smooshed the pans together to get the correct total number of pieces. The pan on the left gave us the value in the numerator and the pan on the right gave us the value of the denominator.


Many students already knew the algorithm in this pre-IB class and jumped right to it. We talked about switching the division sign to multiplication and flipping the second fractions. I refer to this as the “ol’ flip n’ switch”.

I would have liked to have more practice questions for the class to try independently, but we don’t have a textbook and there wasn’t enough time to make anything. I did, however, have the time recently to make a Boom deck for extra practice on this method of simplifying fractions. I am looking forward to using it in my class this fall. You can find the deck here.
That is all for today.
I hope something here was able to help you in your teaching journey.
Have a great day!