March 21, 2022.
Today was our first day back after spring break. We worked on an extensive review since we will have to write the second part of our cycle 1 test this week.

We started today’s warm-up with a Would You Rather activity. Students worked through which option they would rather buy.
Next, we looked at this pizza fundraiser question. My colleague made the question, but ironically my daughter did in fact bring home this fundraiser from her before and after school program. Of course, we had to order pizza, crazy bread, and cookie dough:) The class was randomly put into groups and worked on the large vertical whiteboards to solve the question.

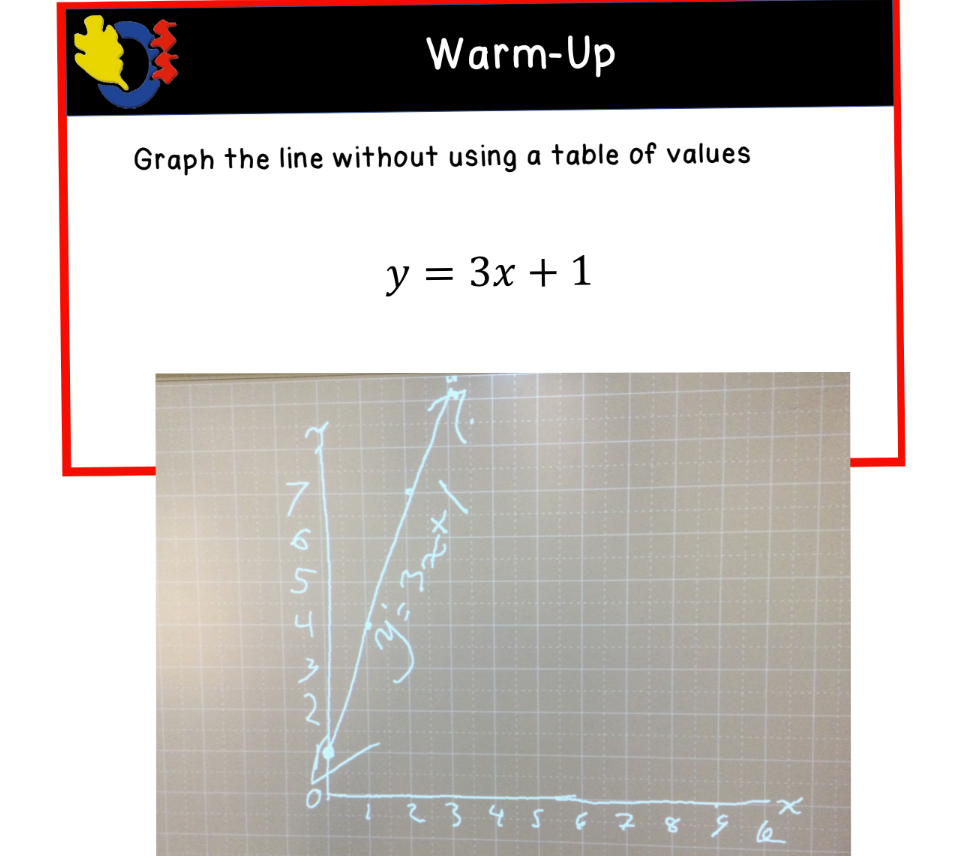
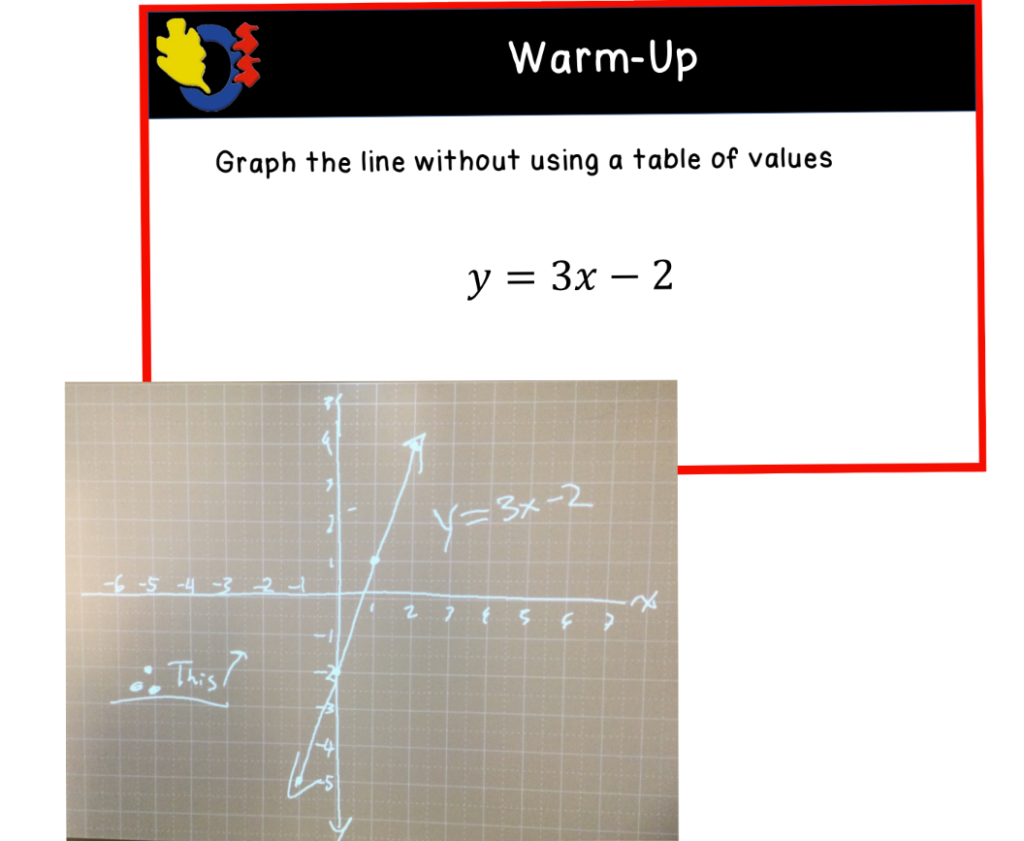
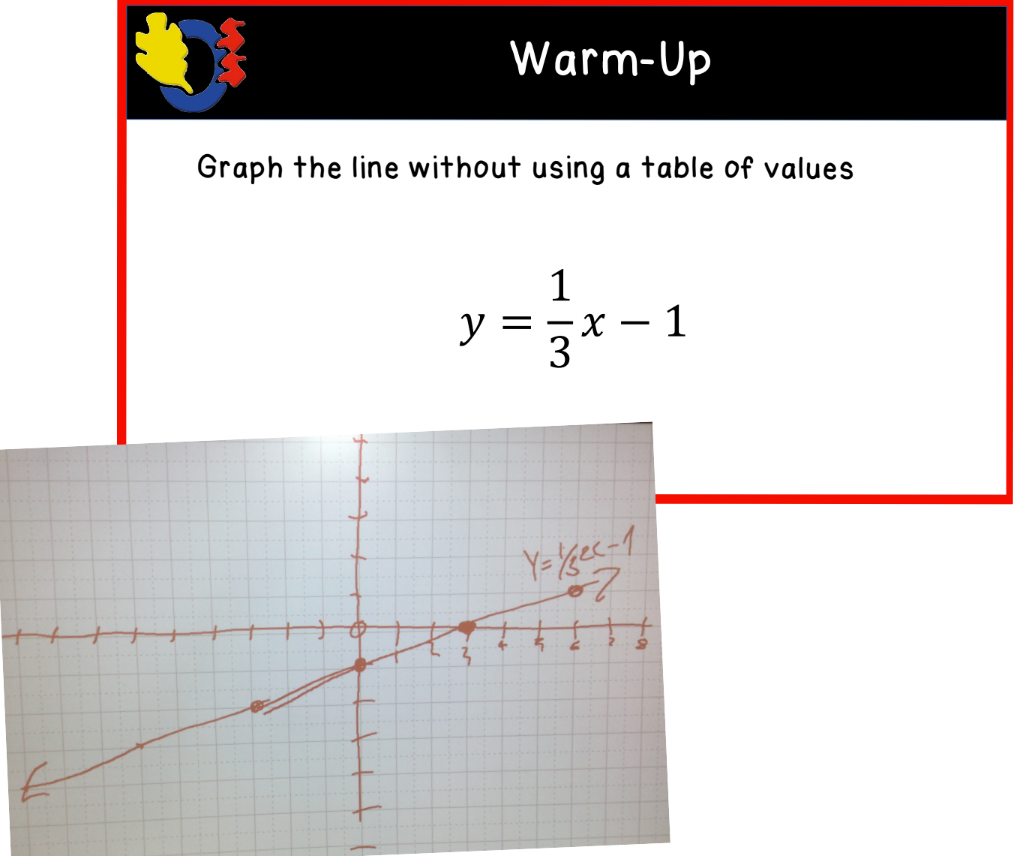
Next, we switched gears and reviewed how to graph a line without using a table of values. Students needed to remember to plot the y-intercept first and use the rate of change to get more points on the line. All of the examples we looked at had positive slopes, and the third example had a fractional slope.
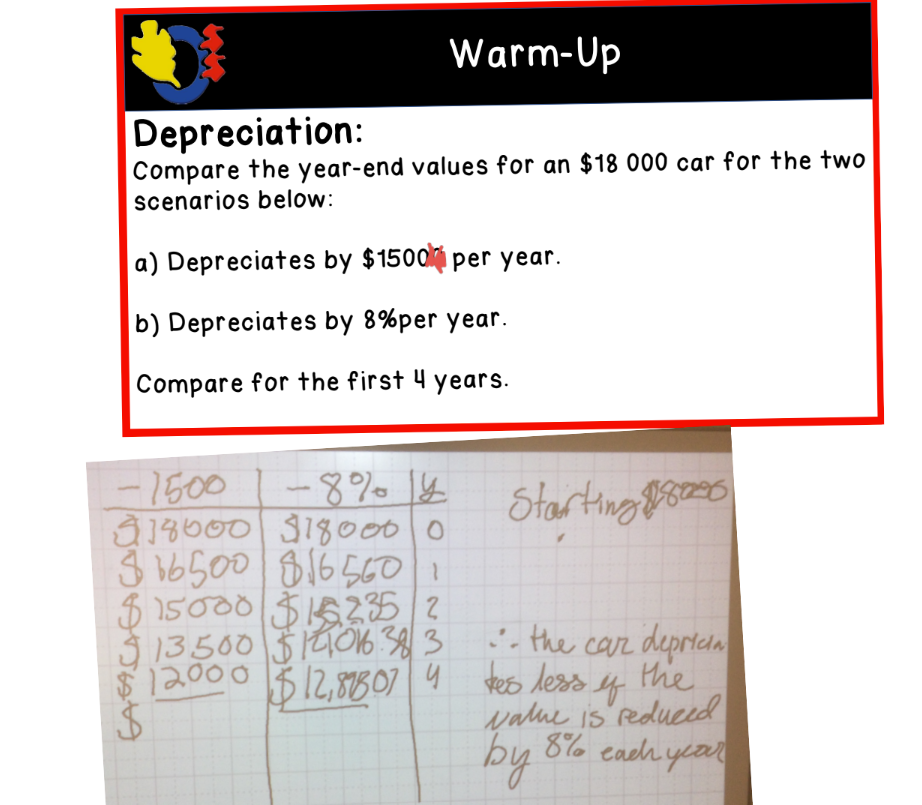
Next, we looked at a depreciation problem. Most groups organized their solution in a table and were able to make a conclusion based on their calculations.

The last warm-up problem we looked at was a unit fraction problem. There were lots of great examples from groups. Here is one of them.
For today’s lesson, we brainstormed different shapes. We talked about regular vs. irregular shapes. This was an excellent segue to calculating the measure of each angle of a regular polygon.

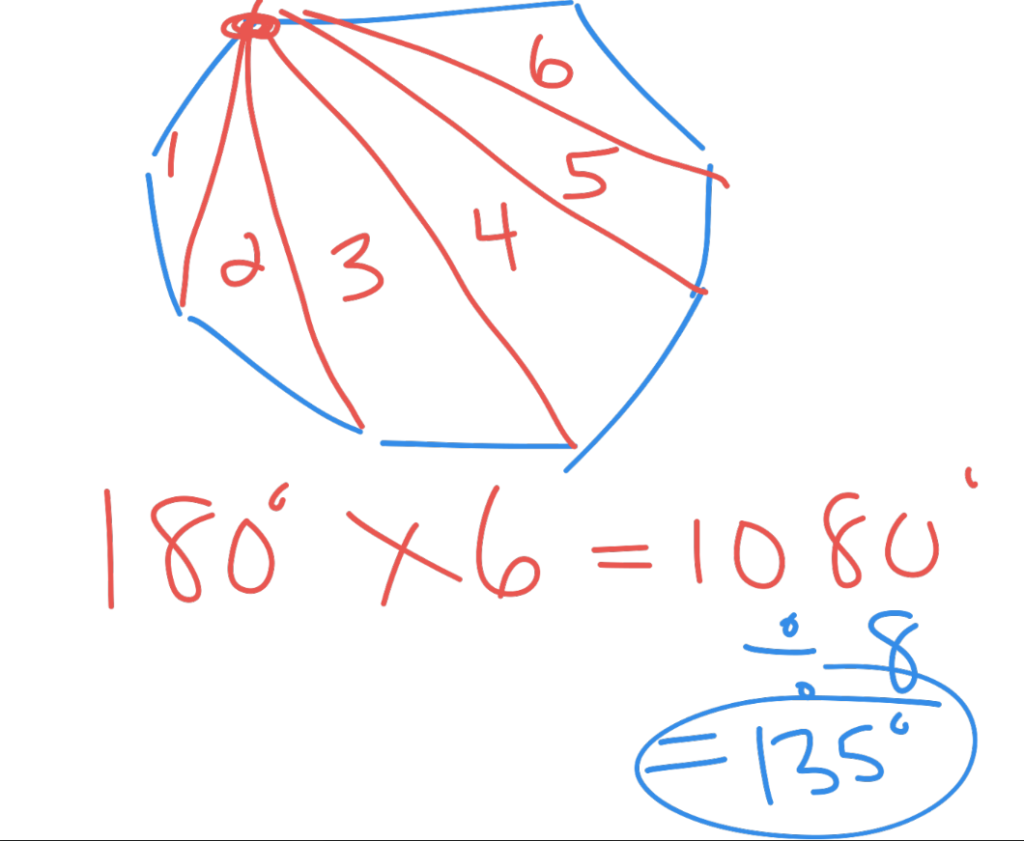
I had students start with the “easy” right-angled shapes and determine the total sum of the interior angles of the polygon and then they were able to tell me the measure of each interior angle. We chose one vertice and drew triangles until all of the sides were used up. For example, a square has 4 sides, so we can make two triangles. Since each triangle has a sum of 180o the total is 180o x 2 triangles or 360o. To calculate each interior angle, we divide 360o by 4 which is 90o. We can follow the same procedure for any regular polygon. A regular pentagon has 3 triangles, a regular hexagon has 4 triangles, etc. The example above models an example of a regular octagon. As you can see, my diagram skills are top-notch… haha.
That brought us to the end of the period. Tomorrow we will practice this new concept with this sum of interior angles of regular polygons Boom CardsTM deck.
That’s all for today.
I hope something here was able to help you in your teaching journey.
Have a great day!