March 7, 2022.
Friday was a PA day, so we had no classes.

For today’s warm-up, we started with a Would You Rather math problem. This problem had students comparing money. I was impressed with the number of groups that set up tables to organize their information. This problem resulted in great discussion about linear vs non-linear relations.
Next, we moved on to our lesson on Egyptian fractions, which led to unit fractions. I used this post to teach the concept.
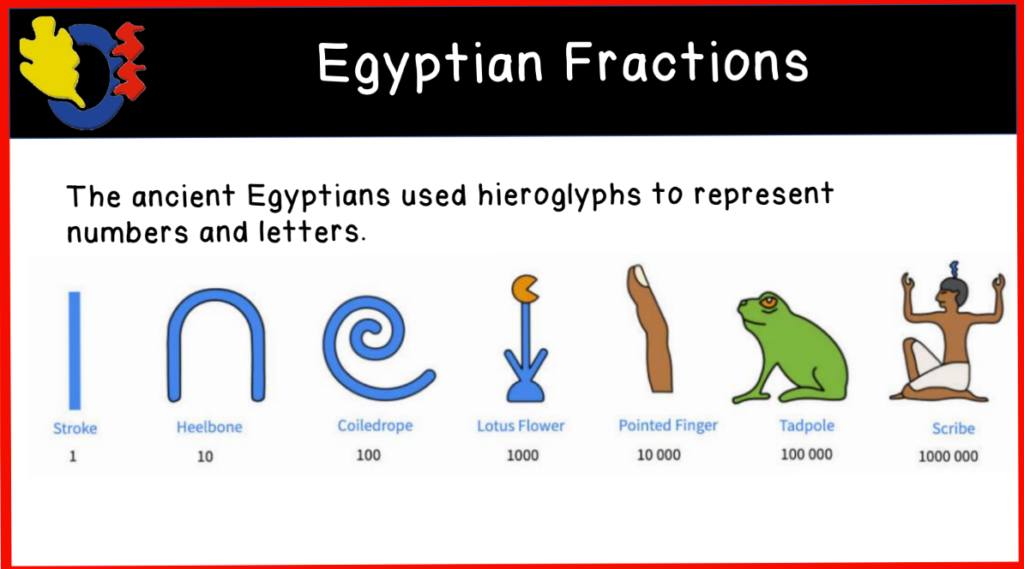




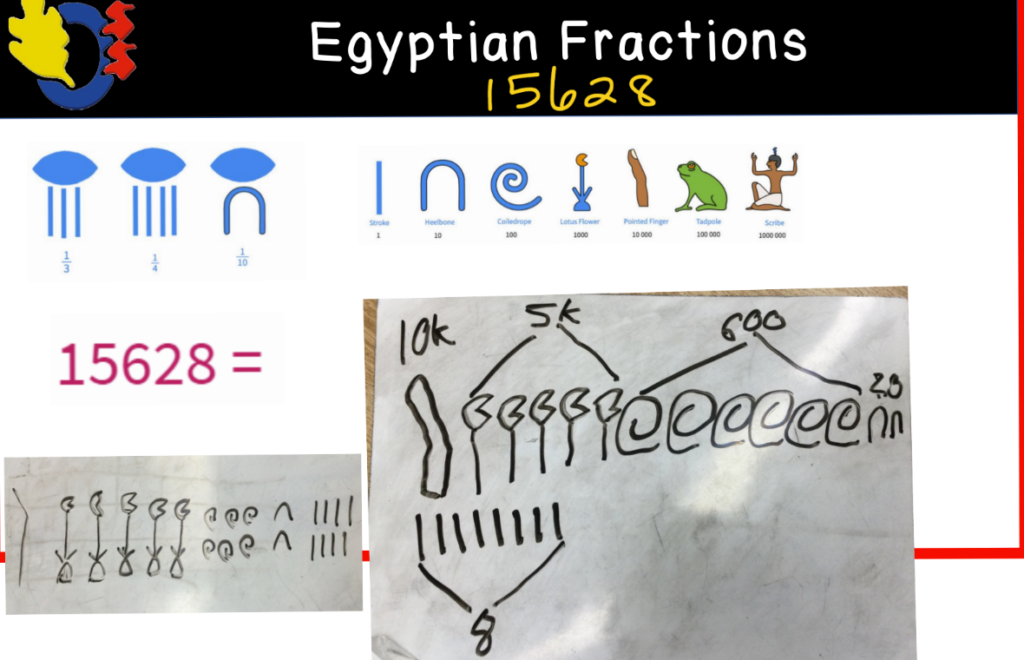
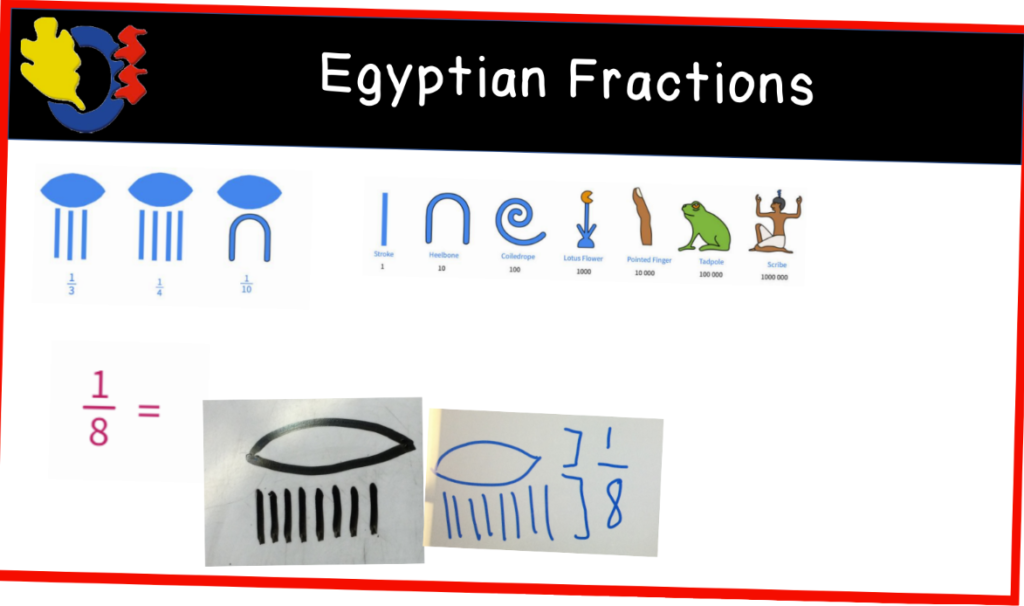

We worked through some fun representations with hieroglyphs. Students started with trying to determine the number or fraction represented by the hieroglyphs and worked toward modeling a number or fraction by drawing the correct hieroglyph.
This was an excellent segue for introducing unit fractions.






We discussed the definition of a unit fraction and looked at a few examples together. The first example we looked at with the fraction tiles was representing 2/3 as a fraction. We chatted about how to use the fraction tiles and get them to match exactly with our representations. We talked about how there could be no gaps, overhangs, etc. for the tile method to work.

Next, I showed the students how to use their calculators to check their solutions. Some of their minds were blown to find out that there was a fractions button on their calculator. Others were disappointed that their calculator didn’t have the button.
We looked at some more examples, so students could get the hang of using the tiles and their calculators.






This part of the lesson went surprisingly fast. Luckily I had some more activities at the ready. Next, we switched gears and looked at a linear relations card sort. I can’t remember where I got the activity, but it had words, tables, linear graphs, and linear equations. This activity also went pretty fast.
We finished the class with some linear graphs to introduce the slope of a line. We looked at several examples where we compared two graphs on one cartesian plane. This activity had students using a lot of vocabulary such as parallel and perpendicular lines, intersecting lines, point of intersection, steepness, positive and negative slopes, etc.
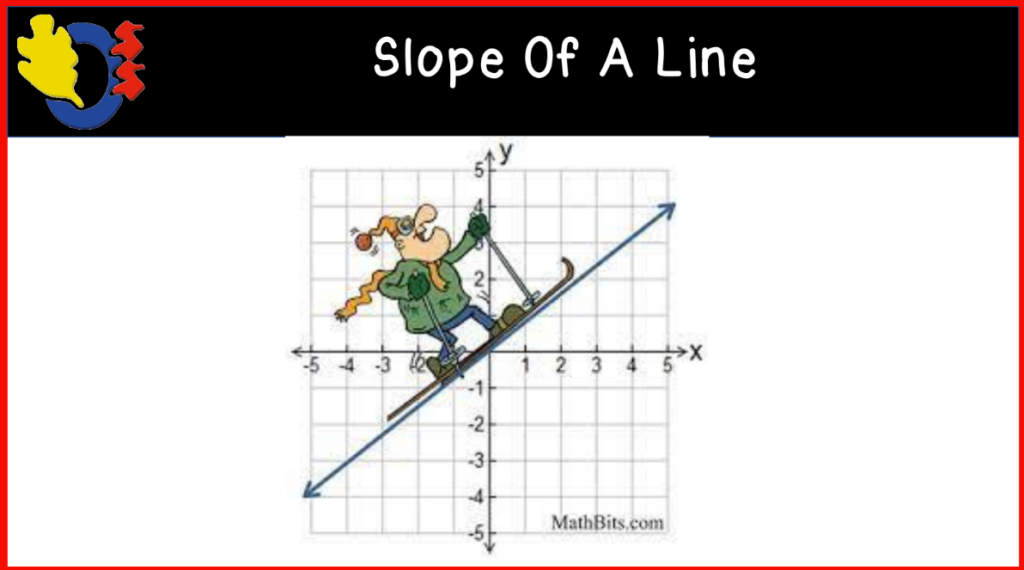
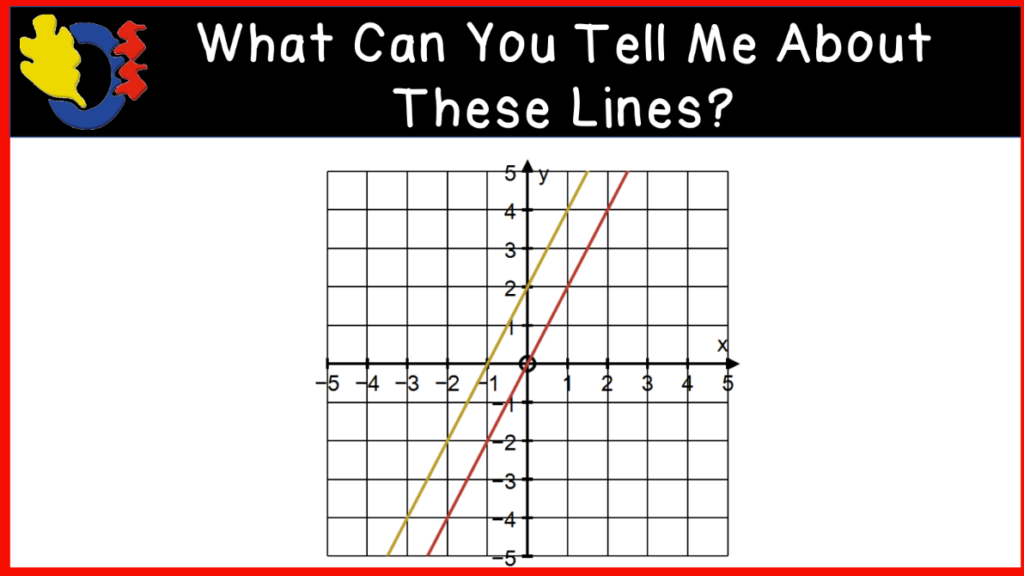
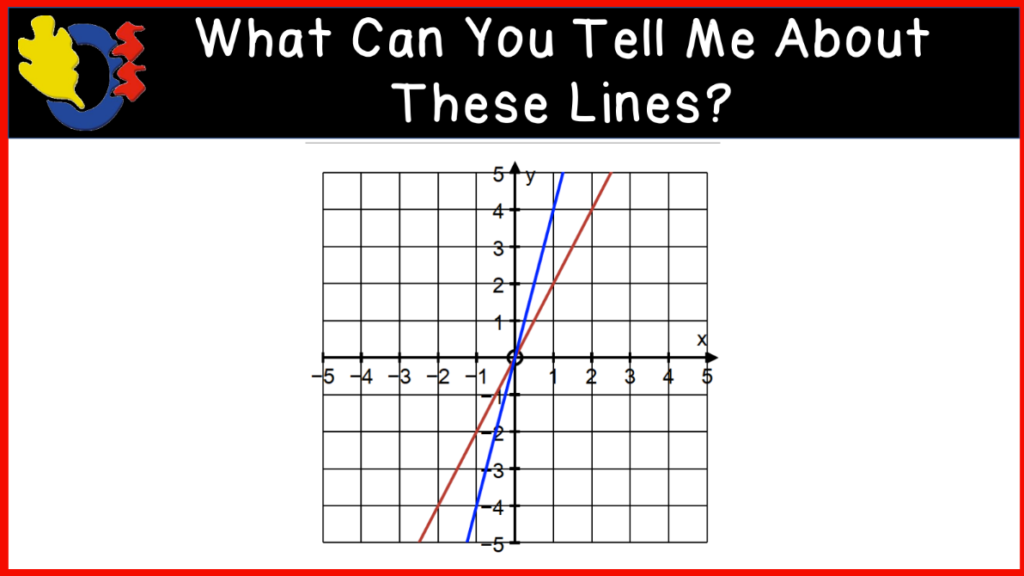
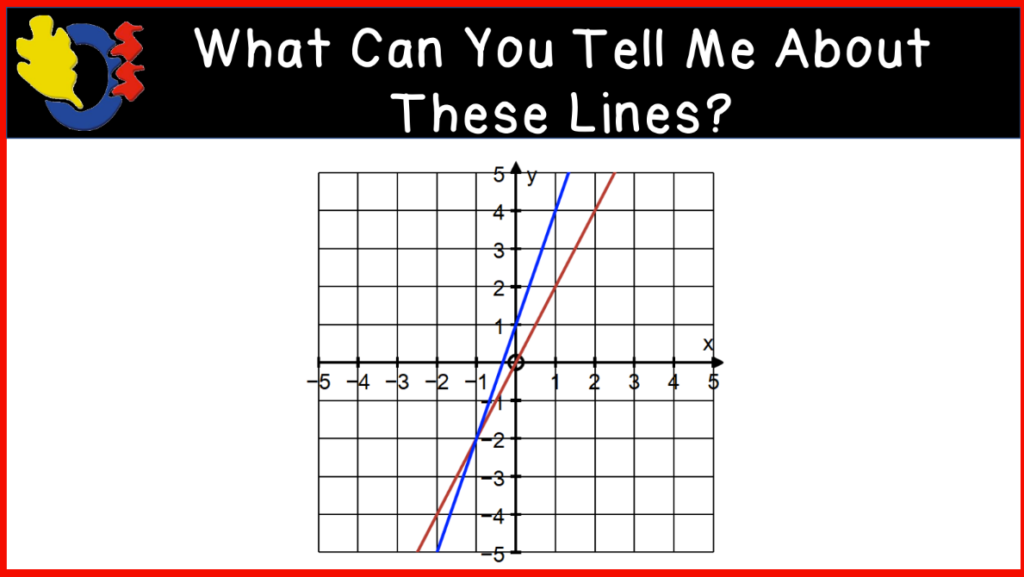
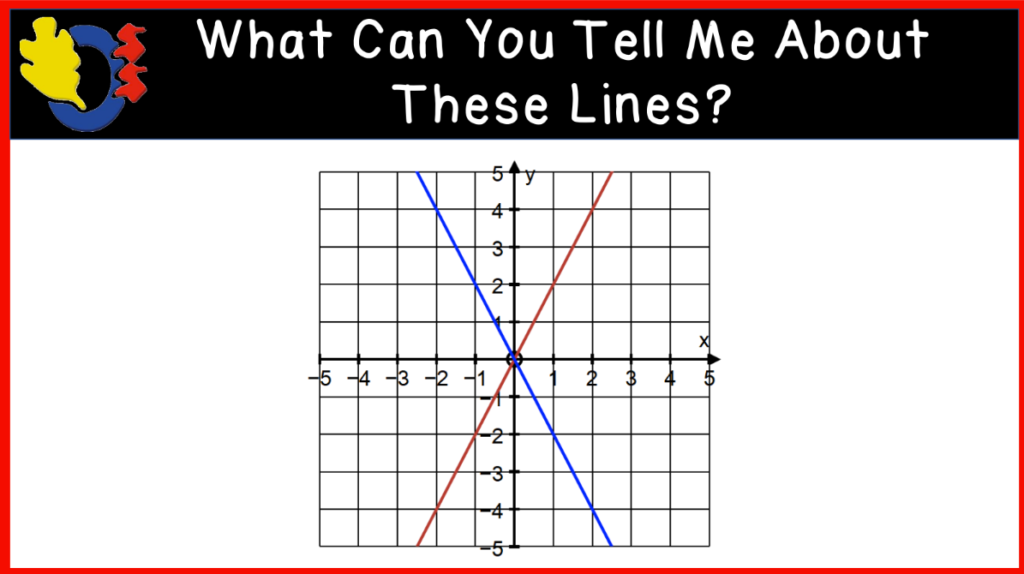
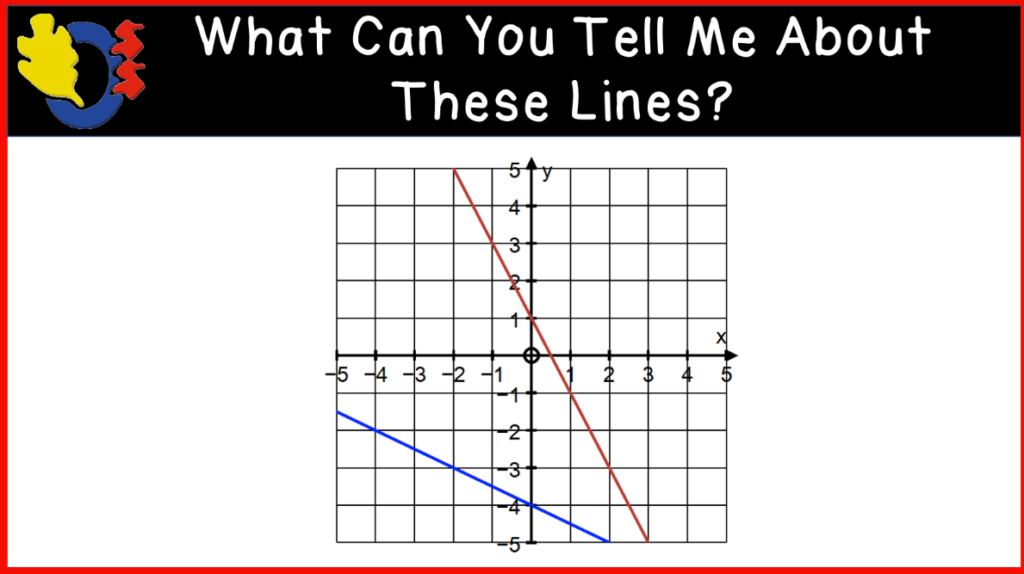
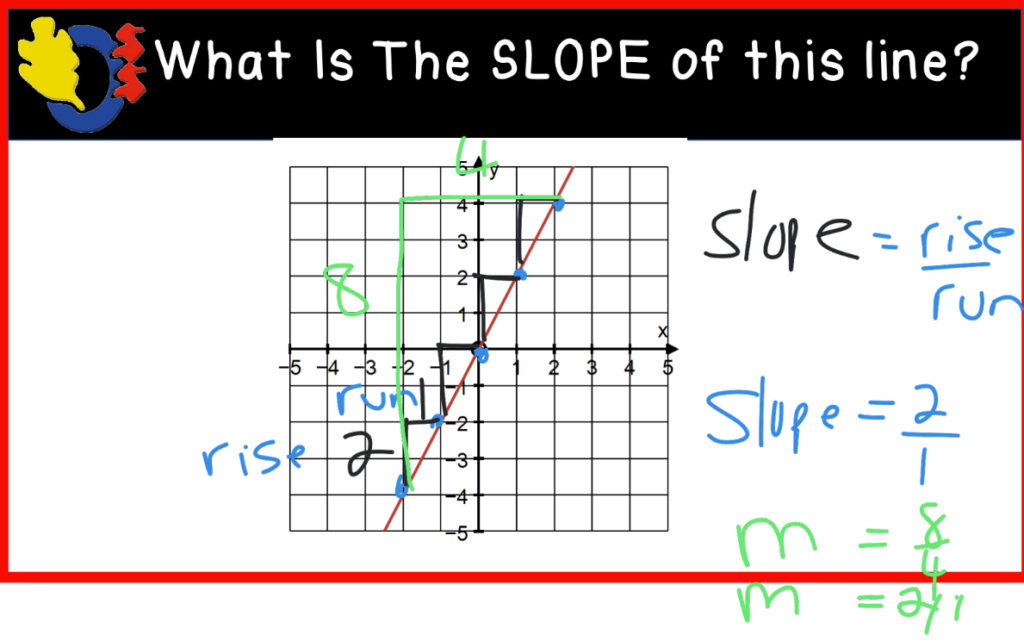
We looked closely at one final graph and drew rate triangles on the line and talked about determining the slope of the line using rise and run. This took us to the bell.
I hope something here was able to help you on your teaching journey.
Have a wonderful day!